箱ひげ図は要約統計量を表示するのに臨床統計でもよくつかわれます。
今回は論文でもよく見られる箱ひげ図をGTLで作図する方法を紹介します。
boxplot
GTLではboxplotステートメントまたはboxplotparmステートメントで作図することができます。
両者の違いについては以下の記事で紹介しています。

boxplotステートメント
boxplot y=y変数 x=x変数 / < options >;
boxplotステートメントはy変数指定するだけで統計量を自動で計算し箱ひげ図を作成できます。x変数は任意で指定できます。x変数を指定した場合、ユニークなXの値毎に箱ひげを作成します。X変数を指定した場合X軸はデフォルトで離散軸となります。
とりあえずSASのサンプルコードに従い各車の燃費を要約して箱ひげ図を作成してみます。
アメリカでは車の燃費はMPG(miles per gallon)で表示するらしいです。
proc template;
define statgraph boxplot;
begingraph; entrytitle "車の燃費比較";
layout overlay /
xaxisopts=(offsetmin=0.1 offsetmax=0.1 label="車種")
yaxisopts=(label="燃費 (miles per gallon)");
boxplot y=mpg_city x=type /
datalabel=make spread=true;
endlayout;
endgraph;
end;
run;
proc sgrender data=sashelp.cars template=boxplot;
run;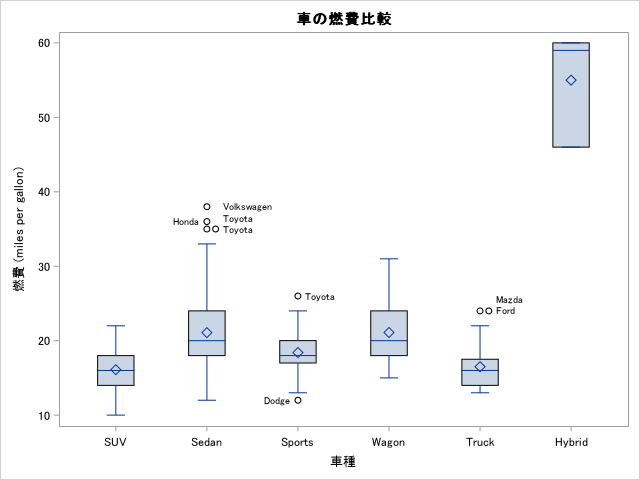
実行結果
boxplotparmステートメント
boxplotparm y=y変数(要約統計量) x=x変数 stat=要約統計量ラベル / < options >;boxplotparmステートメントは作図前にあらかじめ要約統計量を計算する必要があります。
boxplotステートメントの引数に加えて、stat引数が追加されています。statには以下の統計量名を格納します。
- BOXWIDTH( 箱の幅, 0から1の範囲で指定)
- MAX (上側境界以下の最大値)
- MEAN(平均)
- MEDIAN(中央値)
- MIN(下側境界以上の最小値)
- N(データの個数)
- OUTLIER(外れ値:下側境界より小さいデータ、または上側境界より大きいデータ)
- FAROUTLIER(外れ値:25%点-3×IQRより小さいデータ、または75%点+3×IQRより大きいデータ)
- Q1(25%点)
- Q3(75%点)
- STD(標準偏差)
| 統計量名 | 定義 |
|---|---|
| IQR | 4分位範囲(75%点-25%点) |
| 上側境界(upper fense) | 75%点+1.5×IQR |
| 下側境界(lower fense) | 25%点-1.5×IQR |
boxparmステートメントを用いた作図はめんどくさいです。外れ値を検出して外れ値を除いたデータの最大値と最小値を求めないといけません。
ただし統計量と外れ値の算出方法自体は表にまとめる時もあるので覚えておいて損はないでしょう。
具体的にはuniverateプロシジャで四分位数を求め、その値から上側境界(75%点+1.5×IQR)と下側境界(25%点-1.5×IQR)を求め、外れ値を検出します。この境界の範囲外のデータは一般的に外れ値と呼ばれます。
外れ値はデータの分布をみると異常なデータですが、結果を恣意的にゆがめることになりかねないので解析から除外する場合は十分な根拠がある場合に限ります。
データの最大値と最小値は外れ値を除いたデータから算出します。
外れ値を検出するプロシジャがないかどうか探しましたが、見つからなかったのでおそらくマニュアルで求めるしかなさそうです。
今回は統計量算出プログラムを自作して作図データセットを作成しましたが、SASウェブサイトでは同様のデータセットを作成するマクロが公開されています。これを使っても同じことができます。
/* 4分位数を算出 */
proc univariate data=sashelp.cars noprint;
var mpg_city;
class type;
output out=stat
Q1=q1
mean=mean
median=median
Q3=q3
QRANGE=qrange;
run;
/* 上側境界、下側境界を算出(外れ値算出用) */
data stat2;
set stat;
upper=q3+1.5*qrange;
lower=q1-1.5*qrange;
farupper=q3+3*qrange;
farlower=q1-3*qrange;
keep type upper lower farupper farlower;
run;
proc sort data=sashelp.cars out=raw ;
by type;
run;
/* 外れ値とそれ以外を分割 */ d
ata outlier data_minmax;
merge raw stat2;
by type;
if mpg_city < farlower or mpg_city > farupper then do;
STAT="faroutlier";
output outlier;
end;
else if mpg_city < lower or mpg_city > upper then do;
STAT="outlier";
output outlier;
end;
else output data_minmax;
run;
/* 外れ値を除いた最大値と最小値 */
proc univariate data=data_minmax noprint;
var mpg_city;
class type;
output out=minmax
min=min
max=max; run;
/* 作図データ */
/* 四分位数と最大値と最小値をマージ */
data box1;
length stat $20;
merge stat minmax ;
by type;
array st[*] q1 mean median q3 min max qrange;
do i=1 to dim(st);
stat=vname(st(i));
mpg_city=st(i);
output;
end;
keep type stat mpg_city ;
run;
/* 外れ値と統計量データを縦積みする */
data box;
set box1 outlier;
/* データ並び替え用変数 */
select(type);
when("SUV") num=1;
when("Sedan") num=2;
when("Sports") num=3;
when("Wagon") num=4;
when("Truck") num=5;
when("Hybrid") num=6;
otherwise ;
end;
keep num type mpg_city stat make;
proc sort; by num type stat ;
run;
/* テンプレート */
proc template;
define statgraph boxparm;
begingraph;
entrytitle "車の燃費比較";
layout overlay /
xaxisopts=(offsetmin=0.1 offsetmax=0.1 label="車種")
yaxisopts=(label="燃費 (miles per gallon)");
boxplotparm y=mpg_city x=type stat=stat /
datalabel=make
spread=true;
endlayout;
endgraph;
end;
run;
proc sgrender data=box template=boxparm;
run;
(実行結果はboxplotステートメントと同じなので省略)



