Clopper-pearson型の割合の信頼区間は正確な信頼区間と呼ばれ、proc freqを使えば算出することができます。
割合の信頼区間はプロシジャを使わなくてもマニュアルで算出可能です。
Clopper型の割合の信頼区間
正規分布ではなく2項分布に基づいて算出される信頼区間です。標本数が少ない場合であっても被覆確率が設定した信頼水準以上になります。
臨床統計では患者数が必ずしもたくさん調査できるわけではないので、臨床統計では標本数が少ない場合であっても保守的に推定できるClopper-pearson型の信頼区間が良く使われるようです。
算出方法は以下の通りです(F分布を使用した場合)。SASは確率密度に関する関数が用意されているので、プロシジャを使わなくても定義通りに算出することができます。
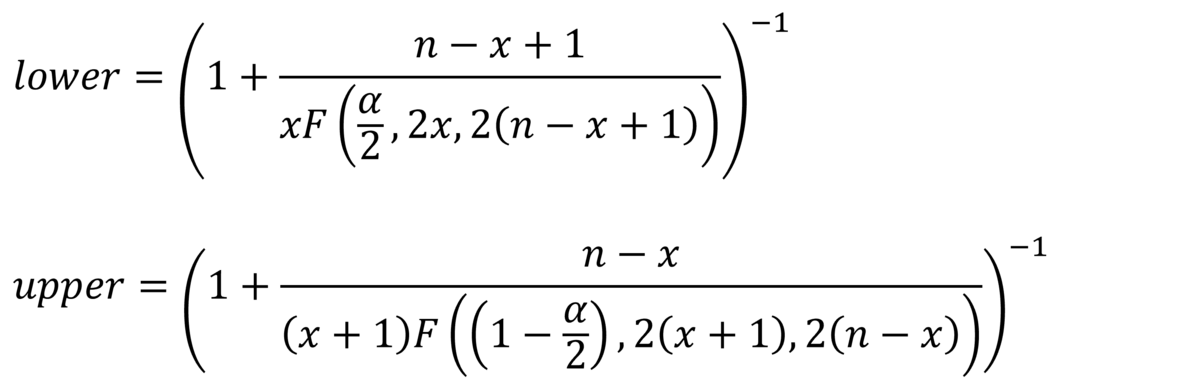
Clopper-Pearson型信頼区間の定義式
ユーザー定義関数
fcmpプロシジャで割合の信頼区間を算出する関数を作ってみました。
一般的にはproc freq のbinomialオプションで算出すると思いますが、自作関数で算出したほうが信頼区間の算出と結果の整形が同時にできるので、こっちのほうが便利なケースが多いんじゃないかな。
今回は信頼下限を算出する関数xlbinと信頼上限を算出する関数xubinを作成してみました。
Copy
/* 分子と分母の標本数から直接正確な信頼区間を計算する */
/* x=分子 */
/* n=分母 */
/* alpha=有意水準 */
proc fcmp outlib=work.func.myfunc;
/* 信頼下限 */
function xlbin(x,n,alpha);
if x^=0 then do;
L=1+(n-x+1) / (x*finv(alpha/2, 2*x, 2*(n-x+1)));
return(L**(-1));
end;
else return(0);
endsub;
/* 信頼上限 */
function xubin(x,n,alpha);
if x^=n then do;
U=1+(n-x) / ((x+1)*finv((1-alpha/2), 2*(x+1), 2*(n-x)));
return(U**(-1));
end;
else return(1);
endsub;
run;テストデータを使って算出してみましょう。標本数60例のうち2例が有害事象を発現したとします。
この時の有害事象発生比率と信頼区間を算出してみます。
options cmplib=work.func;
data test;
r=2/60;
lower=xlbin(2,60,0.05);
upper=xubin(2,60,0.05);
run;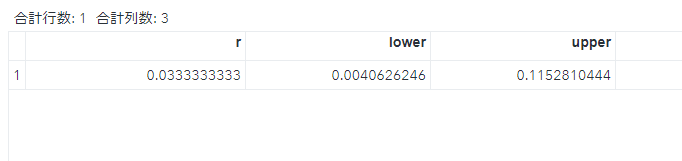
実行結果
proc freq で計算した場合はこうなります。x=1は有害事象あり、x=2は有害事象なし、countは標本数です。proc freqを使う場合はあらかじめ集計する必要があります。
weightオプションで標本数を指定します。このときzerosオプションをいれないと標本数=0となった場合は意図した結果になりませんので必ず入れましょう。
binomialオプションを指定すると正確な信頼区間を算出できます。
BINが比率、XL_BINが正確な信頼下限、XU_BINが正確な信頼上限です。一致しました。
なお比率が0の場合は信頼下限は0、1の場合は信頼上限は1となります。
Copy
/* 検算 */
data dmy;
x=1;
count=2;
output;
x=2;
count=58;
output;
run;
proc freq data=dmy;
tables x / binomial(level=1);
weight count / zeros;
output out=bin binomial;
run;
freq プロシジャのアウトプット

結果の出力例はこちら。パーセンテージに変換して、「(下限-上限)」みたいな形で表示しています。
Copy
data test2;
length res1 res2 $20;
x=13;
n=60;
res1 = strip(put(round(x/n*100, 0.1),5.1));
res2 = "(" || strip(put(round(xlbin(x,n,0.05)*100, 0.1), 5.1)) || "-" || strip(put(round(xubin(x,n,0.05)*100, 0.1),5.1)) || ")";
run;
実行結果
なお信頼区間はベータ分布に基づく計算方法もあります。SASの場合betainv関数を使えば算出できます。betainv関数のみで算出できますが、
比率が0あるいは1の場合は信頼下限または信頼上限は算出できませんので、条件分岐させる必要があります。
data beta;
x=2;
n=60;
/* 信頼下限 */
if x^=0 then
lower=betainv(0.05/2, x, n-x+1);
else lower=0;
/* 信頼上限 */
if x^=n then upper=betainv(1-0.05/2, x+1, n-x);
else upper=1;
run;SAS helpを見る限りproc freqではF分布に基づいて算出しているので、今回はF分布を使用して関数を定義しました。
Rで検算してみる
Rで計算する場合は関数を自作するのも手ですが、PropClsというライブラリのexactCI関数で算出できます。
こちらでも検算してみましょう。
使い方はこちら。使い方は今回自作した関数と同じですが、conf.levelの引数は「1-有意水準」の値を指定する必要があります。また上限と下限をリストの形で出力してくれます。
exactci(x, n, conf.level)
引数
x :分子の例数
n :分母の例数
conf.level :信頼度
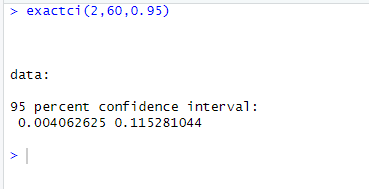
実行結果
あってますね
またstatパッケージのbinom.testを用いても算出できます。検定もできますからこっちのほうが便利かも
binom.test(x, n, p = 0.5, alternative = c("two.sided", "less", "greater"), conf.level = 0.95)
引数
x :分子の例数
n :分母の例数
p:帰無仮説に基づく比率
alternative: 対立仮説、省略した場合はtwo.sided
conf.level :信頼度、省略した場合は0.95結果はリストで出力されます。信頼区間はconf.intに格納されています。
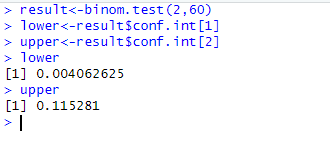
実行結果



