薬物の濃度と生体の応答の関係性は非線形であることが多いため、薬物動態解析や薬理試験では非線形回帰分析を利用されることがあります。
頻繁には実施しないので忘れないようにメモしておきます。臨床だとnlmixedプロシジャかNONMEMを使って非線形混合モデルでの解析が一般的になりつつあると思いますが、今回はラボレベルでは日常的に行われている従来の非線形回帰分析の解析手順をご紹介します。
解析データ
アゴニストを様々な濃度で細胞に処理し(n=3)、その応答を測定します。測定結果から以下のようなデータセットを作成します。
| type | conc | rep | response |
|---|---|---|---|
| 1 | -10 | 1 | 0 |
| 1 | -8 | 1 | 0.0221 |
| 1 | -7.5 | 1 | 0.25 |
| 1 | -7 | 1 | 0.38 |
| 1 | -6.5 | 1 | 0.516 |
| 1 | -6 | 1 | 0.644 |
| 1 | -5.5 | 1 | 0.708 |
| 1 | -5 | 1 | 0.696 |
- type: 1=薬剤処理群 2=コントロール群
- conc: アゴニスト濃度(常用対数)
- rep: 例数(1,2,3)
- response: 生体の応答(吸光度または、LC-MS/MSなどで測定した指標物質の濃度など)
モデル式
アゴニスト濃度と生体の応答の関係性はシグモイド曲線として表現できます。
モデル式は以下の通り。いわゆる4パラメータモデルです。*1
Emaxは薬物による最大応答のことです。(maximum effect)
logEC50は最大応答の50%に達するために必要な薬物濃度の常用対数です。(50% effective concentration)
bottomはシグモイド曲線の下方漸近線を定義します。slopeはシグモイド曲線の傾きを定義します(hill係数)。
パラメータの初期値を求める
非線形回帰分析は線形の回帰分析と同じようにモデルと実測値の差の二乗和を最小にするパラメータを推定しますが、非線形の場合は、二乗和がほとんど変化しなくなる(=収束)までパラメータの修正を繰り返す方法で推定します。
そのため最初にパラメータに代入する初期値が必要になるのですが、設定値は解析者が決めなければなりません。
今回の場合、データが適切に取得できていればEmaxは測定された応答の最大値、bottomは測定された応答の最小値、EC50はアゴニストの設定濃度の中央値とすることが適切でしょう。
slopeは1が標準的な値なので1を代入します。
まずは各群の応答の最大値、最小値および濃度の中央値を求めます。
proc means data=raw;
var response conc;
class type;
output out=ds1(where=(_TYPE_^=0)) max(response)=max min(response)=min median(conc)=median;
run;次にnlinプロシジャに読み込ませるパラメータデータセットを作成します。変数parameterには推定したいパラメータ名を、変数estimateにはパラメータの初期値を格納します。
data pdat;
set ds1;
length parameter $20;
parameter="emax";
estimate=max; output;
parameter="bottom";
estimate=min; output;
parameter="logEC50";
estimate=median;
output;
parameter="slope";
estimate=1;
output;
keep type parameter estimate;
run;パラメータの推定
nlinプロシジャを用いてパラメータデータセットと測定結果からEmaxとEC50を推定します。この時EC50の推定値は対数変換された値なので、実数値に戻す処理が必要となります。plotsオプションでfitplotを指定すると、回帰曲線と実測値をプロットしてくれます。
proc nlin data=raw plots= fitplot ;
parameters / pdata=pdat;
model abs=bottom+(emax-bottom) / (1+10**((logec50-conc)*slope));
by type;
run;パラメータの値がとりえる範囲がわかる場合はboundsステートメントでパラメータの推定値に制約条件を設けるとよいかもしれません。例えばemaxは明らかに0以上であるので制約条件を以下のように設定することができます。
bounds emax>0;
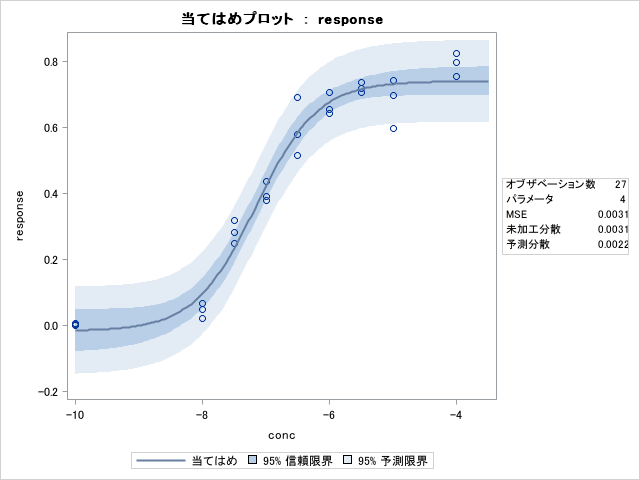
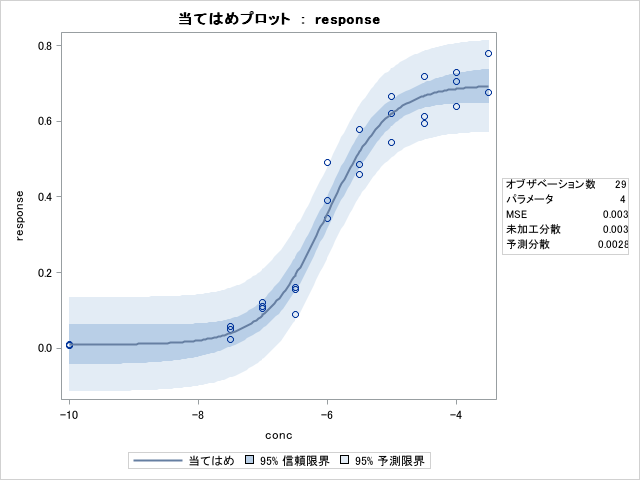
データの確認
非線形回帰分析において、推定結果をプロットすることと、パラメータの信頼区間を確認することはとても大事なので必ず実施しましょう。
実測値と予測値の比較
plotsオプションで出力したプロットを見て、実測値と予測値のずれを見ます。今回は推定した回帰曲線と実測値はおおよそ一致していることがわかります。ほかにも残差プロットをみて残差が正規分布に従っているかどうかを見るのも良いかと思います。
信頼区間
パラメータの推定値の信頼区間が極端に広い範囲でないかどうかを確認します。
| パラメータ | 推定値 | 近似標準誤差 | 近似 95% 信頼限界 | |
|---|---|---|---|---|
| emax | 0.7409 | 0.0214 | 0.6966 | 0.7852 |
| bottom | -0.0164 | 0.0321 | -0.0828 | 0.0499 |
| logec50 | -7.1579 | 0.0805 | -7.3243 | -6.9914 |
| slope | 0.8967 | 0.1266 | 0.6347 | 1.1587 |
| パラメータ | 推定値 | 近似標準誤差 | 近似 95% 信頼限界 | |
|---|---|---|---|---|
| emax | 0.6961 | 0.0242 | 0.6461 | 0.7460 |
| bottom | 0.00942 | 0.0261 | -0.0443 | 0.0631 |
| logec50 | -6.0109 | 0.0843 | -6.1845 | -5.8373 |
| slope | 0.8975 | 0.1399 | 0.6095 | 1.1856 |
今回は信頼区間が狭く推定結果は良好だと判断します。
データが不足していたりモデルとデータがあっていない場合、信頼区間が極端に大きくなり、反復計算が正常に終了していても正しく推定できないことがあります。
試しにTYPE=1の測定結果のうち濃度が-7未満のデータだけで解析すると。ログには「収束基準は満たされましたが、モデルに何らかの問題が存在する可能性があります。」と表示されます。

| パラメータ | 推定値 | 近似標準誤差 | 近似 95% 信頼限界 | |
|---|---|---|---|---|
| emax | 80.7836 | 101.0 | -166.4 | 328.0 |
| bottom | 0.00331 | 0.0139 | -0.0307 | 0.0373 |
| logec50 | -6.0000 | . | . | . |
| slope | 1.6384 | 0.3705 | 0.7319 | 2.5449 |
emaxの信頼区間下限がマイナスになっています。またlogEC50は推定できませんでした。これはemax付近の情報が不足しているため、パラメータの推定に失敗していることを意味します。
こうなった場合はモデル式を変更するか、データ取得をやり直す必要があります。たいていの場合は濃度設定が不適切だったことが原因なので、解析結果をみて設定濃度を修正しましょう。

*1:ベースライン補正しているので今回はbottomは不要でした。次の記事で修正しています。


